Diego Armando Quispe Mollo: julio 2011

Cientifico (133Wx110H) - Cientifico con su probeta que se transforma con su pocima.

Laboratorio quimica (223Wx162H) - Un laboratorio es un lugar equipado con diversos instrumentos de medida o equipos donde se realizan experimentos o investigaciones diversas, según la rama de la ciencia a la que se dedique.

Análisis dimensional

Contenido

1 Procedimiento para el análisis dimensional
2 Aplicaciones del Análisis dimensional
3 Un ejemplo de Análisis dimensional
4 Enlaces externos

Procedimiento para el análisis dimensional

El análisis dimensional es una potente herramienta que permite simplificar el estudio de cualquier fenómeno en el que estén involucradas muchas magnitudes físicas en forma de variables independientes. Su resultado fundamental, el teorema de Vaschy-Buckingham (más conocido por teorema

Π

) permite cambiar el conjunto original de parámetros de entrada dimensionales de un problema físico por otro conjunto de parámetros de entrada adimensionales más reducido. Estos parámetros adimensionales se obtienen mediante combinaciones adecuadas de los parámetros dimensionales y no son únicos, aunque sí lo es el número mínimo necesario para estudiar cada sistema. De este modo, al obtener uno de estos conjuntos de tamaño mínimo se consigue:

analizar con mayor facilidad el sistema objeto de estudio
reducir drásticamente el número de ensayos que debe realizarse para averiguar el comportamiento o respuesta del sistema.

El análisis dimensional es la base de los ensayos con maquetas a escala reducida utilizados en muchas ramas de la ingeniería, tales como la aeronáutica, la automoción o la ingeniería civil. A partir de dichos ensayos se obtiene información sobre lo que ocurre en el fenómeno a escala real cuando existe semejanza física entre el fenómeno real y el ensayo, gracias a que los resultados obtenidos en una maqueta a escala son válidos para el modelo a tamaño real si los números adimensionales que se toman como variables independientes para la experimentación tienen el mismo valor en la maqueta y en el modelo real. Así, para este tipo de cálculos, se utilizan ecuaciones dimensionales, que son expresiones algebraicas que tienen como variables a las unidades fundamentales y derivadas, las cuales se usan para demostrar fórmulas, equivalencias o para dar unidades a una respuesta.
Finalmente, el análisis dimensional también es una herramienta útil para detectar errores en los cálculos científicos e ingenieriles. Con este fin se comprueba la congruencia de las unidades empleadas en los cálculos, prestando especial atención a las unidades de los resultados.

Procedimiento para el análisis dimensional

Para reducir un problema dimensional a otro adimensional con menos parámetros, se siguen los siguientes pasos generales:

Contar el número de variables dimensionales n.
Contar el número de unidades básicas (longitud, tiempo, masa, temperatura, etc.) m
Determinar el número de grupos adimensionales. El número de grupos o números adimensionales ( $Π$ )es n - m.
Hacer que cada número $Π$ dependa de n - m variables fijas y que cada uno dependa además de una de las n - m variables restantes (se recomienda que las variables fijas sean una del fluido o medio, una geométrica y otra cinemática; ello para asegurar que los números adimensionales hallados tengan en cuenta todos los datos del problema).
Cada $Π$ se pone como un producto de las variables que lo determinan elevadas cada una a una potencia desconocida. Para garantizar adimensionalidad deben hallarse todos los valores de los exponentes tal que se cancelen todas las dimensiones implicadas.
El número $Π$ que contenga la variable que se desea determinar se pone como función de los demás números adimensionales.
En caso de trabajar con un modelo a escala, éste debe tener todos sus números adimensionales iguales a las del prototipo para asegurar similitud.

Aplicaciones del Análisis dimensional

Detección de errores de cálculo.
Resolución de problemas cuya solución directa conlleva dificultades matemáticas insalvables.
Creación y estudio de modelos reducidos.
Consideraciones sobre la influencia de posibles cambios en los modelos, etc.

Un ejemplo de Análisis dimensional

Calculemos mediante Análisis Dimensional la velocidad de un cuerpo en caída libre. Sabemos que dicha velocidad

v

dependerá de la altura

h

y de la gravedad

g

. Pero imaginemos que también se nos ocurre decir que la velocidad depende de la masa

m

. Una de las bondades del Análisis Dimensional es que es "autocorregible", es decir, el procedimiento, por sí sólo, elimina las unidades que no son necesarias.

Identificar las magnitudes de las variables:

$\displaystyle [v] = m/s = LT^{-1} \atop {\displaystyle [g] = m/s^2 = LT^{-2} \atop {\displaystyle [h] = m = L \atop {\displaystyle [m] = kg = M}}}$ .

Formar la matriz
Hacer el producto de matrices:

Aquí tenemos que decir que $\displaystyle \epsilon_k$ se refiere al exponente de la unidad $\displaystyle k$ , pero eso se verá en pasos sucesivos.
$\begin{bmatrix}{0}&{0}&{0}&{1}\\{1}&{1}&{1}&{0}\\{0}&{-2}&{-1}&{0}\end{bmatrix}\begin{bmatrix}{\epsilon_h}\\{\epsilon_g}\\{\epsilon_v}\\{\epsilon_m}\end{bmatrix} = \begin{bmatrix}{0}\\{0}\\{0}\end{bmatrix}$ .

Desarrollar el producto de matrices y resolver el sistema de ecuaciones.

Se forma un sistema de ecuaciones. Si nos fijamos, tenemos 4 incógnitas, y sólo 3 ecuaciones, así que para que el sistema pueda ser resuelto, necesitamos tantas incógnitas como ecuaciones. ¿Cómo se subsana el problema? Muy sencillo: se coge un $\displaystyle \epsilon_k$ cualquiera y le asignamos el valor que queramos, a excepción del 0. En nuestro caso, vamos a tomar $\displaystyle \epsilon_v$ como $\displaystyle 1$ .
$\begin{Bmatrix}{\epsilon_m = 0}\\{\epsilon_h + \epsilon_g + \epsilon_v = 0}\\{-2\epsilon_g -\epsilon_v = 0}\end{Bmatrix}$
Si aplicamos la solución inicial que hemos propuesto anteriormente ( $\displaystyle \epsilon_v = 1$ ), se realizan los sencillos cálculos y llegamos a las soluciones:
$\displaystyle \epsilon_h = -1/2$
$\displaystyle \epsilon_g = -1/2$
$\displaystyle \epsilon_v = 1$
$\displaystyle \epsilon_m = 0$

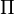
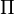Formar el/los grupos $\displaystyle \Pi$

Un grupo $\displaystyle \Pi$ es una ecuación adimensional. ¿Cuántos grupos 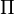$\displaystyle \Pi$ vamos a obtener? 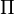Pues si $\displaystyle m$ es el número de unidades (las unidades son el metro, el kilo, el segundo, el grado, ...), y $\displaystyle h$ el rango máximo de la matriz que contiene los coeficientes de las magnitudes de las unidades (a veces coincide el rango de la matriz con el número de variables que tenemos, aunque ésta no es una regla fiable), el número de grupos $\displaystyle \Pi$ (o ecuaciones que obtendremos) será 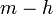$\displaystyle m-h$ . En el caso que nos ocupa, $\displaystyle 4-3 = 1$ ecuación.
Ahora se cogen las unidades que hemos tomado en nuestro problema y las elevamos a los exponentes que hemos obtenido. Ésa es nuestra ecuación.
$\displaystyle \Pi = h^{-1/2}g^{-1/2}v^{1}m^{0} = \frac{v}{\sqrt{gh}}$
(Nótese que 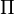$\displaystyle \Pi$ es adimensional). Aquí obtenemos aquéllo que llamábamos "autocorrección": el exponente de la masa es 0, así que desaparece de nuestra ecuación, demostrando una vez más que la caída libre no depende de la masa del objeto en cuestión.

Paso final: obtención de la ecuación.

$\displaystyle v = k \sqrt{gh}$ , con $\displaystyle k$ valiendo $\displaystyle \sqrt{2}$ , lo que nos da la fórmula correcta: $\displaystyle v = \sqrt{2gh}$

Enlaces externos

Ejercicios de Ecuaciones Dimensionales

1. Deducir la ecuación dimensional de las siguientes magnitudes: 1- Velocidad; 2- aceleración; 3- fuerza; 4- constante de gravitación universal; 5- constante dieléctrica K; 6- número p; 7- razones trigonométricas (seno, coseno, tangente).

2. El tiempo que tarda un objeto en caer, en caída libre y sin rozamiento, puede depender de la masa del cuerpo, m, de la altura de caída, h, y de la aceleración de la gravedad, g. Encuentre la dependencia con dichas magnitudes.

3. Deducir utilizando el análisis dimensional los valores de n y m en las siguientes expresiones:

Siendo a la aceleración de una partícula que describe un movimiento circular uniforme, k, una constante adimensional, r el radio de la circunferencia, v el módulo de la velocidad lineal en la primera expresión y T, el periodo de un péndulo simple, l, su longitud y g la aceleración gravitatoria en la segunda.

4. Si se cumple la expresión

. Siendo

intensidad de corriente eléctrica, ¿Qué dimensiones tendrá RC?

5. Al calcular el trabajo, W, realizado por una fuerza encontramos la siguiente expresión.

averiguar si es correcta.

6. Tenemos dos expresiones: 1) y = y0 sen (w .t) y

, donde y e yo son longitudes, t tiempo y w es frecuencia angular (inverso de tiempo). Explique cuál de las dos es incorrecta.

7. El potencial eléctrico producido por una carga puntual, q , en un punto situado a una distancia r de dicha caga se expresa así:

Demuestre que la expresión, V=k.s.r donde s es una densidad superficial de carga (carga/superficie) puede ser cierta.

8. Demuestre que la expresión

en la que V es una diferencia de potencial eléctrico y l y r son longitudes tiene algún error.

9. A partir de la ley de Coulomb

, determine las unidades SI de ε0.

10. La potencia de una hélice impulsora de un barco es

, donde, w = velocidad angular, r = radio de la hélice, D, densidad del agua del mar. Halle x, y, z.

11. De la ley de la atracción universal de las masas,

, halle la ecuación dimensional de K.

12. Fuerza centrípeta depende de la masa, la velocidad y del radio de giro del cuerpo en rotación. Halle la formula correcta para a fuerza centrípeta.

13. La formula de Bernoulli para medir la energía de un líquido que discurre es:

,donde h, altura; p, presión; ρ, densidad; v, velocidad; g, aceleración de la gravedad; w, peso. Verifique el principio de homogeneidad dimensional.